Ciclos de actividad magnética superpuestos y el número de manchas solares: Previsión del ciclo de manchas solares 25 Amplitud

El Sol exhibe una modulación bien observada en el número de manchas en su disco durante un período de aproximadamente 11 años. Desde los albores de la astronomía observacional moderna, las manchas solares han presentado un desafío a la comprensión: su variación cuasi periódica en número, observada por primera vez hace 175 años, ha estimulado el interés de toda la comunidad hasta el día de hoy. Un gran número de técnicas son capaces de explicar los puntos de referencia temporales, la forma (geométrica) y la amplitud de los «ciclos» de manchas solares, sin embargo, predecir estas características con precisión de antemano sigue siendo difícil de alcanzar. Estudios recientes motivados por observación han ilustrado una relación entre el ciclo magnético de 22 años (Hale) del Sol y la producción de los puntos de referencia y patrones del ciclo de manchas solares, pero no la amplitud del ciclo de manchas solares. Utilizando Hilbert transforma (discreto) en más de 270 años de números (mensuales) de manchas solares, identificamos sólidamente los llamados eventos de «terminación» que marcan el final del ciclo anterior de manchas solares de 11 años, la mejora / aceleración del ciclo actual y el final de los ciclos de actividad magnética de 22 años. Utilizando estos extraemos una relación entre el espaciado temporal de los terminadores y la magnitud de los ciclos de manchas solares. Dada esta relación y nuestra predicción de un evento de terminación en 2020, deducimos que la mancha solar Solar Cycle 25 podría tener una magnitud que rivaliza con los pocos primeros desde que comenzaron los registros. Este resultado estaría en marcado contraste con la estimación de consenso comunitario de la magnitud 25 del Ciclo Solar de las manchas solares.

El flujo y reflujo (decenal) (depila y disminución) en el número de manchas oscuras en el disco solar ha motivado literalmente miles de investigaciones desde el descubrimiento del ciclo de manchas solares de 11 años casi periódico del mismo nombre por (Schwabe, 1844, Figura 1). Desde entonces, se ha hecho hincapié en determinar la física subyacente de la producción de manchas solares (p. ej. Charbonneau, 2010, 2014; Brun et al., 2015; Cameron, Dikpati y Brandenburg, 2017), además de predecir numéricamente las propiedades de los próximos ciclos utilizando estadísticas (p. ej. Pesnell, 2018; Pesnell y Schatten, 2018) o métodos físicos (p. ej. Upton y Hathaway, 2018; Bhowmik y Nandy, 2018). En las últimas décadas, a medida que la amplitud y el momento del ciclo de manchas solares ha alcanzado una mayor importancia social, se han convocado paneles de toda la comunidad y se han encargado de construir opiniones de consenso sobre el próximo ciclo de manchas solares, varios años antes del próximo pico (Pesnell, 2008). La falta de restricciones adecuadas, los supuestos contradictorios relacionados con el mecanismo de dinamo solar y las diferentes técnicas, a salvo de decir, dan lugar a una amplia gama de presentaciones a estos paneles que cubren casi todos los posibles resultados «físicamente razonables» (Pesnell, 2016; Petrovay, 2020).

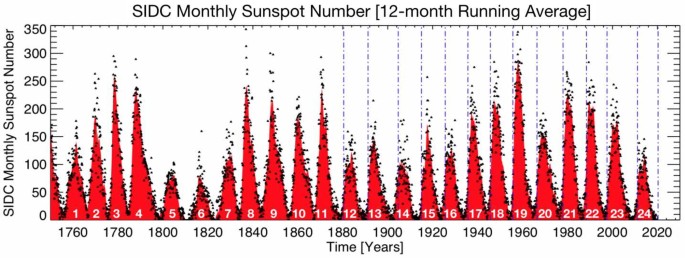
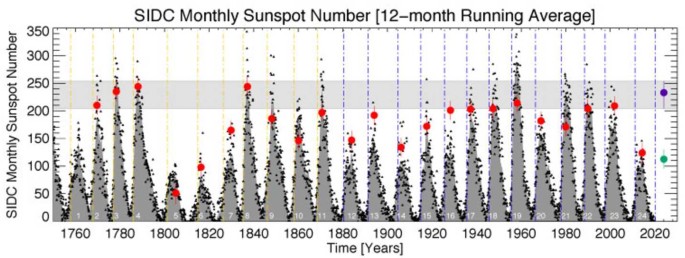
El número mensual de manchas solares desde 1749. Los valores de datos están representados por puntos y los valores promedio de ejecución de 12 meses se ilustran como un área sombreada en rojo. Los números de ciclo de manchas solares se muestran en el área sombreada: el número 1 comienza en 1755 y el número 24 que actualmente está llegando a su fin. También se muestra en la figura un conjunto de líneas discontinuas azules verticales que significan los tiempos de terminación del ciclo de actividad magnética que desencadenan el rápido crecimiento de la actividad de las manchas solares (McIntosh et al., 2019). Los datos de manchas solares utilizados aquí están disponibles gratuitamente y son proporcionados por el World Data Center-SILSO del Real Observatorio de Bélgica. Hemos utilizado la versión 2.0 del número de manchas solares (Clette et al., 2014, 2015) que está disponible en este sitio web, identificado como el «Número total de manchas solares media mensual»: http://www.sidc.be/silso/.

La predicción del ciclo de manchas solares es un negocio de alto riesgo y se ha convertido en un evento decenal, comenzando oficialmente para el Ciclo Solar 23 (Joselyn et al., 1997), y repetido para el Ciclo Solar 24 (Pesnell, 2008), el esfuerzo reunió a una gama de expertos en la materia y una serie de métodos presentados que van desde precursores de campos magnéticos polares, a través de modelos numéricos, y también utilizando climatologías observadas para extrapolar en el tiempo (p. ej. Petrovay, 2020). Vale la pena señalar que el método del «precursor del campo polar», que utiliza mediciones del campo magnético polar del Sol al mínimo solar para predecir la próxima intensidad del ciclo de manchas solares, demostró ser preciso para el Ciclo Solar 24 (p. ej. Svalgaard, Cliver y Kamide, 2005; Schatten, 2005) y ha informado gran parte de la ciencia que ha seguido.

El Ciclo 25 de Manchas Solares no es diferente en términos de apuestas, trayendo algunos de los pronósticos de modelos físicos más sofisticados a la discusión, además de los métodos robustos y refinados motivados por datos, el Panel de Predicción del Ciclo Solar 25 copresidido por la NOAA/NASA (en adelante, SC25PP) entregó el siguiente pronóstico de consenso: El Ciclo de Manchas Solares 25 (en adelante, en adelante, SC25) será similar en tamaño al Ciclo 24 de Manchas Solares (en adelante, SC24). El máximo de SC25 no se producirá antes del año 2023 y a más tardar en 2026 con un número máximo de manchas solares máximaNota¹ de 95 y un número máximo de manchas solares pico de 130. Por último, el panel espera que el final de la SC24 y el inicio de la SC25 ocurran no antes de julio de 2019 y a más tardar en septiembre de 2020.

McIntosh et al. (2014) (en adelante M2014) infirieron que el ciclo de manchas solares podría describirse en términos de las interacciones (magnéticas) de las bandas toroidales polarizadas opuestas, espacio-temporalmente superpuestas del ciclo de actividad magnética de 22 años del Sol, o Hale (véase, por ejemplo, la Figura 2). Esas interacciones de banda tienen lugar dentro de un hemisferio solar y a través del ecuador solar. Además, afirmaron que el grado en que las bandas magnéticas en el sistema se superponen temporalmente define la amplitud máxima de un ciclo de manchas solares, la suposición es que debe haber una cantidad suficiente de campo magnético desequilibrado local (o globalmente) para formar boyantemente una mancha solar. Por lo tanto, las épocas para las que el tiempo de superposición de la banda es corto darían lugar a ciclos de alta amplitud y, a la inversa, para épocas de superposición de banda más larga. Esto tal vez se ilustra mejor en la Figura 2 y teniendo en cuenta la naturaleza de los mínimos de manchas solares, cuatro bandas polarizadas opuestamente están dentro de la latitud del ecuador, anulando efectivamente la capacidad del Sol para formar manchas.

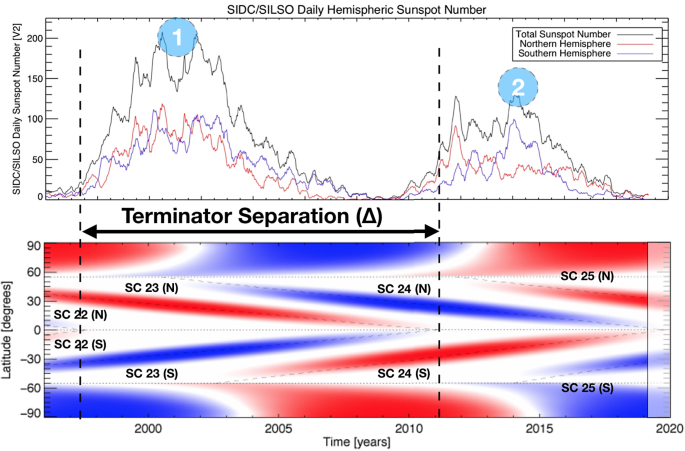
Se infiere latitud versus evolución temporal de las bandas de actividad magnética y los eventos de terminación del ciclo de Hale de 22 años en los últimos 22 años. Arriba: Número hemisférico y total de manchas solares de los últimos Ciclos 23 y 24. Las líneas verticales muestran los eventos de terminación de los Ciclos Solares 22, 23 y (predichos) 24, que son seguidos por un rápido aumento de la actividad solar. Abajo: Un dibujo conceptual de las bandas de actividad hipotéticas de M2014 que son la estructura subyacente del ciclo solar extendido. La separación indicada entre los terminadores del Ciclo Solar 22 y 23 proporciona un predictor para la amplitud del Ciclo Solar 24, mientras que la separación entre el terminador del Ciclo Solar 23 observado y el terminador del Ciclo Solar 24 predicho proporciona un método para predecir el Ciclo Solar 25. Las etiquetas numeradas en el panel superior son ilustrativas para el lector y los dos experimentos que llevaremos a cabo a continuación.

La época inmediatamente posterior a las condiciones mínimas del ciclo de manchas solares surge cuando las dos bandas de latitud más bajas se cancelan: la terminación (McIntosh et al., 2019, en adelante M2019). En la imagen de M2014, la terminación de las antiguas bandas productoras de manchas solares en el ecuador solar ocurre al final de su viaje de 19 años desde la latitud ≈5555 y ve al Sol sufrir un cambio significativo en la actividad magnética global en la escala de una sola rotación solar. La terminación señala el final de un ciclo de manchas solares (y magnéticas) y el inicio del siguiente ciclo de manchas solares en latitudes medias, reconociendo que las bandas restantes del ciclo magnético en cada hemisferio han estado presentes durante varios años antes de la terminación (véase, por ejemplo, la Figura 2) y el proceso que resulta en la inversión del campo magnético polar del Sol.

M2014 exploró solo los últimos 60 años de actividad solar, con solo los ciclos solares posteriores incluyendo un alto volumen de datos EUV, por lo que hubo poco intento de cuantificar la relación entre la superposición de banda, la interacción y la amplitud de los ciclos de manchas solares. En la imagen de M2014, la separación temporal de los eventos de terminación se puede utilizar como medida de la superposición de banda. M2019 extendió ese análisis a otro siglo de tal manera que 13 ciclos de manchas solares tuvieron sus eventos terminadores identificados; vea las líneas discontinuas azules verticales en la Figura 3 y la Tabla 1.

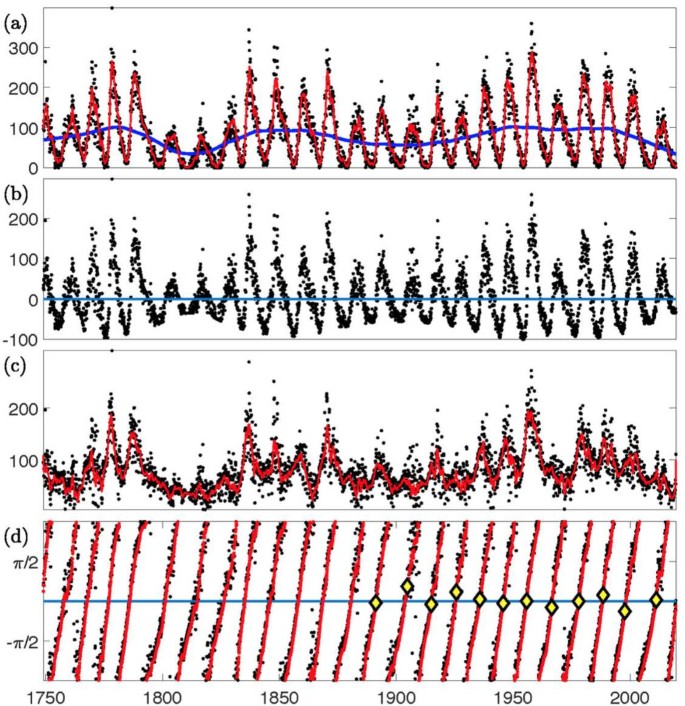
Hilbert discreta transforma el número mensual de manchas solares desde 1749. De arriba a abajo: (a) Número mensual de manchas solares (negro), promedio móvil de 12 meses (rojo) y tendencia de escala de tiempo lenta obtenida por regresión local usando mínimos cuadrados lineales ponderados en una ventana de 40 años (azul); (b) número de manchas solares mensual con tendencia de regresión local restada; (c) amplitud de señal analítica de promedio móvil mensual (negro) y 12 meses (rojo) número de manchas solares; (d) fase de señal analítica como en (c), los diamantes amarillos indican terminadores obtenidos previamente McIntosh et al. (2019). Los tiempos de terminación utilizados aquí son los cruces analíticos de fase cero.

Después de M2019, Leamon et al. (2020) exploraron un enfoque algorítmico para la identificación de eventos de terminación en datos de manchas solares y proxy de actividad. Esto se logró explotando las propiedades de la discreta transformación de Hilbert (Marple, 1999). Identificaron que los proxys de actividad mostraban una propiedad común en que las funciones de amplitud y fase que resultan del pico discreto de transformación de Hilbert y experimentan un volteo de fase idéntico en los terminadores, identificando básicamente los cambios más rápidos en las series temporales. Verificaron los eventos de terminación identificados por M2014 y utilizaron su enfoque algorítmico para extender el registro del terminador hasta 1820 (Ciclos Solares 7-24), utilizando el registro histórico de manchas solares recientemente actualizado (Clette et al., 2014, 2015). La Figura 3 muestra el número de manchas solares mensuales reconstruidas (Clette et al., 2015) en el que basaremos el análisis presentado aquí, explotando la discreta transformación de Hilbert para explorar la relación entre la superposición de la banda del ciclo de actividad magnética (a través de la separación del terminador) y la amplitud de los ciclos de manchas solares (resultantes).

La transformación de Hilbert

Para una serie temporal dadaS(t)S(t)podemos obtener una señal analítica (Gabor, 1946)A(t)exp[iφ(t)]=S(t)+iH(t)A(t)exp[iφ(t)]=S(t)+iH(t)dondeH(t)H(t)es la transformación de Hilbert (Bracewell, 2000) deS(t)S(t)yA(t)A(t)yφ(t)φ(t)son la amplitud y fase analítica de la señal, respectivamente. Para una señal discreta como el número mensual de manchas solares analizadas aquí, se puede construir una señal analítica discreta a partir de la transformación discreta de Fourier de la señal original. Hemos utilizado un método estándar (Marple, 1999) que satisface tanto la invertibilidad como la ortogonalidad, como se implementa en la función hilbert de Matlab. Hay formas alternativas de definir fases instantáneas y amplitudes del ciclo solar consideradas por Mininni, Gómez y Mindlin (2002). Sin embargo, concluyeron que el enfoque de señal analítica es el mejor.

Aunque se define para una serie temporal arbitraria, la señal analítica solo dará una descomposición físicamente significativa de la serie temporal original si la frecuencia instantáneaω(t)=dφ(t)/dtω(t)=dφ(t)/dtsigue siendo positivo (Boashash, 1992). Por lo tanto, para una señal positiva-definida como el número mensual de manchas solares, necesitamos eliminar una tendencia de fondo (ver Chapman et al. (2018) para un ejemplo, y más discusiones en Pikovsky et al. (2002), Boashash (1992) y Huang et al. (1998)). Obtuvimos una tendencia que varía lentamente al realizar una regresión lineal local robusta que reduce los valores atípicos («rlowess») utilizando la función suave de Matlab con una ventana de 40 años.

Determinación de las fechas de Terminator

Utilizamos el método discutido en Chapman et al. (2020) y Leamon et al. (2020) para determinar nuestra evaluación de las fechas de terminación a través de la fase analítica de la transformación discreta de Hilbert. Para un segmento finito dado de una serie temporal, la transformación discreta de Hilbert produce una diferencia en la fase analítica en relación con la de alguna hora de inicio (arbitraria). Para mayor comodidad aquí hemos establecido la fase cero en el terminador para el inicio de la mancha solar Ciclo Solar 24 (McIntosh et al., 2019). En la construcción de la Figura 3 primero realizamos un promedio móvil de 12 meses del número mensual de manchas solares y luego calculamos la señal analítica discreta correspondiente. La fase analítica de la señal se interpoló linealmente para obtener los cruces de fase cero y los tiempos de terminación correspondientes. Las diferencias entre los sucesivos tiempos de terminación no dependen de la elección de la fase cero.

Realizar un análisis discreto de la transformación de Hilbert y la identificación del terminador (ver Leamon et al., 2020) pero con el registro mensual (en lugar del diario) de manchassolares y con la resta de una tendencia que varía lentamente en el tiempo como se muestra en el panel a de la Figura 3, permite la expansión de la serie temporal del terminador hasta 1749. De hecho, dicho análisis cubre el mínimo de Dalton (de 1790 a 1830, o SC5 a SC7) además de las épocas de alta actividad a finales de los años 1700, 1850 y 1950. En resumen, este período muestra muchas de las actividades solares extremas a lo largo del tiempo de observación y catalogación humana detallada. La Figura 3a muestra el número mensual de manchas solares desde 1749 hasta el presente, según la Figura 1. La curva roja muestra una versión suavizada de 12 meses de la serie temporal. La curva azul que se muestra en la Figura 3a muestra el suavizado de regresión local de la serie temporal de manchas solares, donde la ventana de suavizado se elige para ser de 40 años. La eliminación de la tendencia de manchas solares suavizadas de las series temporales suavizadas mensuales y de 12 meses resulta en las series temporales que se muestran en la Figura 3b. En Leamon et al. (2020) aplicamos la transformación discreta de Hilbert a las dos series temporales restadas por tendencias de manchas solares para revelar las funciones de amplitud y fase correspondientes de la transformación discreta de Hilbert en las Figuras 3c y 3d, respectivamente. La aplicación del suavizado de regresión local a las series temporales resulta en una transformación discreta de Hilbert que mantiene una función de fase de valor real. En contraste con la aplicación de Leamon et al. (2020), hemos establecido que la función de fase de la transformación discreta de Hilbert sea idénticamente cero en el terminador de 2011, lo que significa que los cruces cero de la función de fase, que también coinciden con los máximos en la función de amplitud, significan terminadores en las series temporales. Como referencia, los terminadores de M2014 y M2019 se indican como diamantes amarillos. Observe la fuerte correspondencia entre los terminadores M2014 y M2019 y los derivados de forma independiente aquí utilizando los datos de manchas solares más gruesos (mensuales).

La aplicación de esta metodología duplica efectivamente el número de terminadores disponibles para un estudio extendido. Una comparación visual de la Figura 3d y 3a sugiere una relación entre la separación de los terminadores y las amplitudes del ciclo de manchas solares: los ciclos de manchas solares de baja amplitud parecen corresponder con terminadores ampliamente separados, mientras que los ciclos de manchas solares de mayor amplitud corresponden a terminadores más separados estrechamente. La Tabla 1 proporciona las amplitudes del ciclo de manchas solares, las fechas de terminación y la longitud del ciclo de manchas solares derivada de la separación de los eventos del terminador (ΔTΔT) que se derivan de las Figuras 1 y 3.

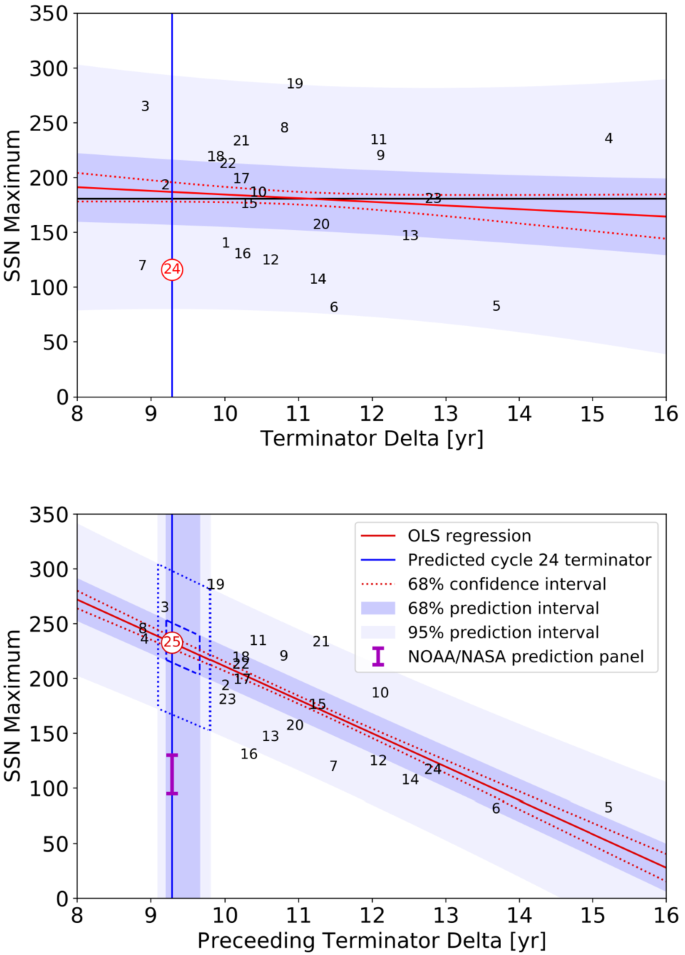
Para explorar esta comparación visual, analizamos la relación entreΔTΔTy la amplitud de ese ciclo de manchas solares y el próximo (es decir, el próximo) ciclo de manchas solares (ver Figura 2). Como se demostró en el panel superior de la Figura 4, no encontramos una correlación significativa entre la separación del terminador y la amplitud del ciclo de manchas solares que contiene. El 68% (1σ1σ) se muestra que contiene la amplitud del número medio de manchas solares (SSN) de pendiente cero (línea negra), lo que indica que la hipótesis nula de correlación cero no se rechaza.

Observando las relaciones entre la separación del terminador y las amplitudes del ciclo de manchas solares. Regresiones lineales de la separación del terminador frente a (comparación 1; panel superior) máximo de manchas solares de ciclo intermedio y (comparación 2; panel inferior) el siguiente máximo de ciclo de manchas solares. El1σ1σ(68%) intervalo de confianza, así como el1σ1σ(68%) y2σ2σ(95%) se muestran intervalos de predicción. La separación del terminador prevista para SC24 se muestra en ambos paneles, lo que junto con la línea de regresión resulta en una predicción de la amplitud de SC25 en el panel (b) que es significativamente mayor que la predicción de consenso de la SC25PP (barra de magenta). La línea horizontal negra en el panel superior es la media del máximo del SSN, mientras que las líneas azules discontinuas y punteadas en el panel inferior son los límites del intervalo de predicción del 68% y 95% para la predicción SC25, respectivamente.

Compare ahora la separación del terminador y la amplitud del próximo ciclo de manchas solares que se muestra en el panel inferior de la Figura 4. Una regresión ordinaria de mínimos cuadrados (OLS), muestra una anticorrelación significativa entre las dos propiedades. La línea de regresión esSSNn+1=(−30,5±3,8)ΔTn+516SSNn+1=(−30,5±3.8)ΔTn+516. El coeficiente de correlación de Pearson esr=−0,795r=−0.795y la correlación es significativa hasta el nivel del 99,999%. Estimamos los intervalos de predicción en el 68% (1σ1σ) y 95% (2σ2σ), que también se trazan en el panel inferior de la Figura 4.

Utilizando una predicción de temporización del terminador SC24 de Leamon et al. (2020) de2020.37+0,38−0,08(1σ)2020.37−0,08+0,38(1σ)junto con nuestra línea de regresión e intervalos de predicción, nuestra mejor estimación para la amplitud de SC25 es SSN=233, con una confianza del 68% en que la amplitud caerá entre SSN=204 y 254. Utilizando el tiempo de Leamon et al. (2020) esto resultaría en una predicción (con una confianza del 95%) de que la amplitud SC25 caerá entre SSN=153 y 305. En el momento de la aceptación, el terminador de SC24 aún no se ha alcanzado y está alargando la separación del terminador SC23 – SC24. Por lo tanto, las amplitudes SC25 mencionadas deben considerarse preliminares y como valores limitantes que disminuyen en aproximadamente 10 por cada extensión trimestral de año en la separación del terminador. La intención de los autores es presentar una aclaración a la predicción SC25 presentada aquí cuando se produce el terminador SC24.

Para poner estos valores en perspectiva, y para resaltar la fortaleza de la relación desarrollada anteriormente, la Figura 5 ilustra el pronóstico de la SC25 (al nivel de confianza del 68%) en púrpura, en contraste con el del consenso de SC25PP en verde. El rectángulo ligeramente sombreado ayuda a colocar nuestro pronóstico en contraste con los ciclos de manchas solares anteriores, como se proyecta que SC25 estaría entre los cinco primeros de los observados. Además, los puntos rojos en la parcela son reconstrucciones, o un retrodifusión, de las amplitudes máximas solares dados solo los valores medidos deΔTΔTy la relación derivada anteriormente. Con la excepción de subpredecir la amplitud de las SC 10, 19 y 21 (recuerde que los valores utilizados para desarrollar el panel inferior de la Figura 4 se extraen de datos suavizados anualmente) la recuperación de los máximos de manchas solares es muy alentadora, aunque observamos que parece subestimar sistemáticamente los ciclos de manchas solares de mayor amplitud.

Previsión de amplitud del Ciclo de Manchas Solares 25 en contexto. El número medio mensual de manchas solares desde 1749. Los valores de datos están representados por puntos y los valores promedio de 12 meses se ilustran como un área sombreada de gris oscuro. Los números de ciclo de manchas solares se muestran en el área sombreada: SC1 a partir de 1755 y SC24 actualmente está llegando a su fin. Para comparar con la Figura 1 mostramos las líneas discontinuas azules verticales (M2019) que significan los tiempos de terminación del ciclo magnético que desencadenan el rápido crecimiento de la actividad de las manchas solares, mientras que las líneas discontinuas naranjas verticales muestran los terminadores derivados de la transformación de Hilbert de Leamon et al. (2020), ver Figura 3 y la Tabla 1. También se muestran los valores de previsión de amplitud SC25 del análisis anterior (punto púrpura) y el SC25PP (punto verde). La región horizontal compartida gris claro debe colocar el pronóstico actual en contexto histórico. Finalmente, mostramos los máximos de manchas solares de retroceso para cada ciclo (puntos rojos) derivados de los valores de terminación medidos y utilizando la relación desarrollada anteriormente: las barras de error en los puntos de retrodifusión representan el valor de confianza del 68%.

Impacto de suavizar ventanas en las fechas de Terminator

En el desarrollo del material anterior hemos investigado cómo los dos parámetros de suavizado (la escala de tiempo en la que se desarrolla la tendencia y el suavizado de la escala de tiempo más corta aplicado a la serie temporal residual eliminada por la tendencia; «tendencia» y «residual», respectivamente, para abreviar) pueden influir en la determinación del terminador. También consideramos el impacto de la estadística de media de ejecución frente a la baja en la construcción de la tendencia de la serie temporal; para el conjunto de parámetros utilizado en la Figura 3, la diferencia entre los terminadores inferidos entre estos dos enfoques fue del 0,03%.

Teniendo esto en cuenta, y la aplicación de la estadística de rebajo en las cifras anteriores, la usaremos en la estimación del análisis de impacto de suavizado. Con el análisis de Leamon et al. (2020) en mente, hemos variado el ancho de la ventana utilizada en la tendencia (para un rango de 5 a 150 años). Por debajo de 15 años hay cruces de terminadores adicionales (falsos) en fase cero. Por debajo de 35 años hay notables ondas en la tendencia. Más de 125 años vemos que la fase de Hilbert no aumenta monótonamente con el tiempo en lugares de tal manera que ya no resuelve los ciclos de manchas solares más débiles. Este efecto comienza a influir significativamente en el análisis más allá de los 60 años, por lo tanto, utilizaremos un intervalo de 35 a 60 años como rango de trabajo para la eliminación de tendencias donde hay muy poco impacto (<0,1%) en los terminadores derivados y, por lo tanto, las relaciones de la Figura 4.

Del mismo modo, fijando la tendencia a 40 años, hemos estudiado el impacto en la determinación del terminador variando el suavizado residual de 1 a 84 meses. Para el suavizado de series temporales residuales de más de 3 meses, los terminadores y su separación son estables, pero para valores más grandes (>42 meses), las separaciones del terminador y el terminador son más variables. Más allá de los 42 meses, el residuo se suaviza en exceso y deja de parecerse a la serie temporal de entrada original. Más de 84 meses, el método no resuelve los ciclos débiles de manchas solares. Concluimos que el rango de trabajo aplicable para el suavizado residual es de 9 a 30 meses.

El resultado de estos experimentos se puede utilizar para evaluar su impacto en las separaciones del terminador y, por lo tanto, en la relación identificada en el panel inferior de la Figura 4. ElΔTΔTversus relación de máximas manchas solares tiene una pequeña varianza (<2%) y un efecto aún menor en la magnitud proyectada de SC25 (<0,5% a 1σσ, y <0,9% a 2σσ).

Aunque no es un estudio exhaustivo de la literatura, comparamos brevemente la relación separación-amplitud del ciclo del terminador mostrada anteriormente con un trabajo prominente en la literatura que utiliza la separación de mínimos solares como una medida de la longitud del ciclo para desarrollar la previsibilidad de la próxima fuerza del ciclo. Tenemos fuertes reservas sobre esto último dada la discusión anterior sobre la naturaleza superpuesta de los ciclos de Hale, su impacto en el ciclo de manchas solares (M2014), y especialmente en el contexto de las condiciones solares mínimas que resultan de la cancelación mutua de cuatro bandas magnéticas, por no mencionar la subjetividad de la recolección cuando se produce un mínimo de manchas solares (p. ej. Petrovay, 2020).

Se ha observado previamente que la amplitud de un ciclo de manchas solares está anticorrelacionada con la duración del ciclo de manchas solares anterior, medida por la duración del tiempo entre el mínimo de manchas solares y solares (por ejemplo, Chernosky, 1954; Hathaway, Wilson y Reichmann, 1994). Para referencia, el enfoque de Hathaway produjo un coeficiente de correlación de Pearson der=−0,68r=−0,68, mientras que el anterior trabajo solar-mínimo centrado de Chernosky tenía un coeficiente de correlación de Pearson der=−0,71r=−0,71. However, we refer to the introduction (and Figure 2) to point out that the concept of solar minimum is a physically ill-defined quantity whose value depends on the activity record and the smoothing method used (Hathaway, 2015; Petrovay, 2020).

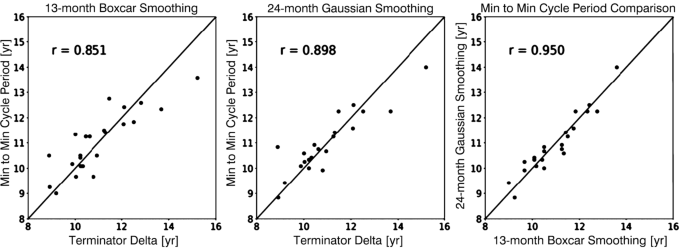
Contrastamos nuestro enfoque adoptado anteriormente con una longitud de ciclo mínima a mínima más tradicional frente a las separaciones del terminador utilizando dos métodos tradicionales de determinación mínima del ciclo suavizado: el suavizado de vagones de 13 meses (con puntos finales de peso medio) tomado de la Tabla 2 de Hathaway (2015) y un suavizado gaussiano FWHM de 24 meses de la Tabla 1 de Hathaway, Wilson y Reichmann (1999). De izquierda a derecha en la Figura 6 comparamos el suavizado del vagón de 13 meses con la separación del terminador, el suavizado gaussiano del vagón FWHM de 24 meses y la comparación de los dos, junto con su respectivo coeficiente de correlación Pearson.

La relación entre la separación del terminador y la separación mínima de manchas solares.Ilustrando las relaciones entre la separación mínima de manchas solares frente a la separación del terminador con diferentes parámetros de suavizado utilizados en la determinación del primero, de izquierda a derecha un método de suavizado de automóviles de caja de 13 meses frente a la separación del terminador, un método de suavizado gaussiano de 24 meses frente a la separación del terminador, y luego la relación entre las dos metodologías de suavizado. En cada caso se muestra el coeficiente de correlación de Pearson.

Como era de esperar, la separación del terminador está bien correlacionada con la duración del ciclo determinada a partir de los métodos más antiguos. Sin embargo, los métodos mínimos de dos ciclos están mejor correlacionados entre sí que con la separación del terminador. Esto indica que no es probable que una regresión para la longitud y amplitud del ciclo mínima a mínima de la próxima amplitud del ciclo mejore para una opción específica del método de suavizado de manchas solares, mientras que la separación del terminador más robusta produce una mejor correlación que la que se encontró en trabajos anteriores.

Para el lector interesado, identificamos varias referencias históricas mientras investigamos esta sección del artículo. Hathaway, Wilson y Reichmann (2002) señalan Chernosky (1954) como trabajo anterior sobre la relación amplitud-duración del ciclo de manchas solares. Chernosky (1954) a su vez, señaló a Wolf (1861) como una fuente anterior sobre la relación para los «ciclos concurrentes» (es decir, como en la Figura 4a), afirmando que era «uno de los descubrimientos más importantes con respecto a las condiciones solares (cf. Ludendorff, 1931). En este artículo utilizamos Chernosky (1954) como un motivador para la idea de un fuerte efecto de amplitud-período para «seguir» los ciclos de manchas solares (i.e. Figura 4b).

Finalmente, comparamos los coeficientes de correlación publicados de Pearson del trabajo publicado en estos artículos anteriores con la relación derivada aquí:

1. i)Este trabajo, el método de separación del terminador para SC1 a SC23 produce un valor r de -0,795.
2. ii)La Figura 29 de Hathaway (2015), utilizando un suavizado de vagones de 13 meses para SC1 a SC23 produce un valor r de -0,68.
3. iii)La Figura 7a de Hathaway, Wilson y Reichmann (2002), utilizando un suavizado gaussiano de 24 meses para SC2 a SC22 produce un valor r de -0,69.
4. vi)La Figura 6 de Hathaway, Wilson y Reichmann (1994), utilizando parámetros de ajuste de la forma del ciclo de manchas solares para SC2 a SC18, produce un valor r de -0,63.
5. v)La Figura 1B de Chernosky (1954), utilizando un suavizado medio de 12 meses para SC5 a SC18 produce un valor r de -0,71.

Por lo tanto, a partir de este estudio limitado de la literatura prominente sobre el tema, vemos que la separación del terminador proporciona un indicador estadísticamente más fuerte de la amplitud del ciclo de las manchas solares, siendo notablemente mejor que los métodos derivados mínimos del solar.

El modelo fenomenológico presentado en M2014, y empleado anteriormente, difiere en un aspecto crítico de los modelos convencionales basados en la física empleados en el SC25PP, esfuerzos similares publicados recientemente (Bhowmik y Nandy, 2018), y ahora para los modelos inspirados en el aprendizaje automático (Kitiashvili, 2020). La característica central común de estos modelos es que los campos magnéticos presentes o generados por ellos son dinámicamente pasivos con respecto a los flujos a gran escala presentes en el sistema (Charbonneau, 2010), o están «congelados», utilizando terminología magnetohidrodinámica (Alfvén, 1942). Por el contrario, una explicación para la activación rápida y sincronizada hemisféricamente de la emergencia de flujo magnético de latitudes medias y altas después de los eventos de terminación en el ecuador solar requiere que las bandas magnéticas del ciclo magnético de Hale sean fuertes y sean dinámicamente importantes en relación con los flujos (McIntosh et al., 2019; Dikpati et al., 2019). Por último, si hubiera una fuerte divergencia entre el pronóstico presentado anteriormente y los que utilizan la metodología del predictor polar (p. ej. Svalgaard, Cliver y Kamide, 2005; Schatten, 2005) deberíamos revisar el papel del campo magnético polar del Sol en el desarrollo del mecanismo de dinamo del Sol.

En los próximos meses, a medida que madure el SC25, se hará evidente cuál de estos paradigmas (muy diferentes) es más relevante, tal es el contraste en las previsiones discutidas aquí. Indicaciones muy tempranas del patrón de manchas están apareciendo en latitudes más altas que el promedio (≈40; Nandy, Bhatnagar y Pal, 2020). Históricamente, la emergencia de manchas de latitudes altas se ha asociado con el desarrollo de ciclos de manchas solares de gran amplitud (p. ej. Waldmeier, 1935,1939; Hathaway, 2015): solo el tiempo dirá cuán precisas son todas estas predicciones para SC25.

Nuestro método predice que SC25 podría estar entre los ciclos de manchas solares más fuertes jamás observados, dependiendo de cuándo ocurra la próxima terminación, y es muy probable que sea ciertamente más fuerte que el SC24 actual (número de manchas solares de 116) y muy probablemente más fuerte que el SC23 anterior (número de manchas solares de 180). Esto contrasta marcadamente con el consenso del SC25PP, el número máximo de manchas solares entre 95 y 130, es decir, similar al de SC24. De hecho, como se puede ver en la Figura 4b, si nuestra predicción para el tiempo de terminación de 2020 es correcta, un valor tan bajo sería un valor atípico severo con respecto al comportamiento observado de ciclos de manchas solares anteriores. Un valor tan bajo solo podría reconciliarse con los ciclos de manchas solares observados anteriormente si el siguiente evento de terminación se retrasa más de dos años desde nuestro valor predicho, lo que extendería los bajos niveles de actividad actuales a una duración extraordinaria. Observamos también que la relación desarrollada aquí habría predicho correctamente la baja amplitud de SC24 (a partir de una separación de terminadores de 12,825 años) después del terminador de 2011, tres años después de que el Panel de Predicción del Ciclo Solar de la NOAA/NASA de 2006 entregara su predicción de consenso (Pesnell, 2008). Finalmente, la llegada del terminador SC24 permitirá una mayor fidelidad en el pronóstico presentado.

Los datos de manchas solares utilizados aquí están disponibles gratuitamente y son proporcionados por el World Data Center-SILSO del Real Observatorio de Bélgica. Hemos utilizado la versión 2.0 del número de manchas solares (Clette et al., 2014, 2015) que está disponible en este sitio web, identificado como el «Número total mensual de manchas solares»: http://www.sidc.be/silso/.

1. Al citar máximos de manchas solares seguimos la convención de paneles de predicción pasados en este manuscrito. A lo largo de todo, citamos el número de manchas solares suavizadas para máximos, un valor que se determina utilizando un suavizado de 13 meses consecutivos del número promedio de manchas solares para cada mes calendario.

2. El lector interesado puede leer el comunicado de prensa oficial de la NOAA que describe el pronóstico del Panel en https://www.weather.gov/news/190504-sun-activity-in-solar-cycle. Sin embargo, observamos que la versión 2.0 del número de manchas solares (Clette et al., 2015) indica que el número máximo de manchas solares suavizadas para el Ciclo Solar 24 fue de 116.

    

   FUENTES: Scott W. McIntosh ,Sandra Chapman,Robert J. Leamon,Ricky Egeland yNicholas W. Watkins